I don't believe that there is a dichotomy between a supposedly modern and traditional architecture. Instead there exist different geometric processes, and while traditionally builders have employed nesting processes in their work, for perhaps no other reason than it came naturally to them, modern builders have restricted themselves to linear geometric processes due to drawing their inspiration from Cartesian science and engineering.

In attempting to transform architecture into a vessel for artistic expression, modern architects have been trapped by their limited tool set, and the product of their work has often been confusing, silly, or utterly corrupt. There are only so many tricks that one can perform with linear geometry, although computers have extended the reach of those tricks. But the confusion of modern architects becomes even more obvious when they ascribe artistic merits to traditional builders who never aspired to be artists at all. One such instance is the introduction of a recent biography of the 18th century french military engineer Vauban by official starchitect Jean Nouvel, who described Vauban's fortresses as an early form of land-art and morphing. Jean Nouvel asks, could a man be an artist without being aware of it? Vauban was not an artist at all. Military necessity led him to employ geometric processes that significantly increased the complexity of fortifications, and it is merely incidental that today we find his projects to have artistic merits.

The process through which Vauban's work became worthy of architectural praise provides the key to the distinction between linear and nesting geometry. Vauban was not himself the inventor of the star fort. Those had been around for more than a century when he began his career for the army of king Louis XIV. The basic star fort was a simple concept: the old masonry walls of the medieval age had shown themselves to be obsolete with the advent of cannons, and they had been replaced with thick banks of earth dug out of trenches whose major flaw was to provide space out of reach of defensive fire at its angles. The angles were thus extended into diamond-shaped turrets in the first pass at a feedback correction, introducing nesting geometry and initiating the first step of the genesis of a fractal.

A basic, early star fort

While the star fort was successful at resisting attacks, it was not impregnable. A method was devised to capture them by digging trenches in zig-zagging patterns through which troops could assault the walls without being exposed to cannon fire. In fact this is how Vauban built his career, and some of his "plans" for besieging star forts are significant civil engineering projects of their own.

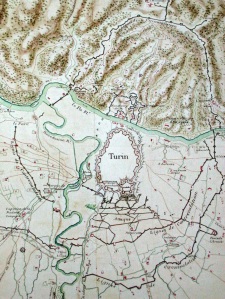
The siege of Turin. From an encircling trench, Vauban built successively denser trenches to capture the citadel and take the city, a process that was extremely expensive and time-consuming.

While star forts never truly became obsolete (as medieval fortifications had) until well into the 19th century, military engineers did improve on their effectiveness by correcting their vulnerabilities, which happened to be at the angles they were characterized by. And so, by another layer of feedback, the geometric depth of the star fort concept increased.

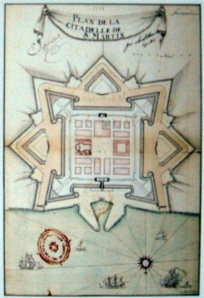
San Martin Citadel, a "second generation" star fort.

Vauban's great invention was nothing much more than repeating this process of increasing depth one more time, creating what many now consider to be his masterpiece, the Citadel of Lille, a showcase of complex geometry made from the refinement produced by centuries of feedback of the star fort concept.

Citadel of Lille and the system of fortification of the City of Lille, as designed by Vauban

If you only understand Cartesian processes, then the only idea that may come to you to improve on the basic star fort would be to add dozens of diamond-shaped turrets, a change that would most certainly make the concept worse instead of better. The military engineers of the time however were well aware that the diamond turrets were optimal in their shape. What was needed was a shape that extended the diamond, and this was achieved by increasing the depth of the whole object.

Another aspect of the complexity of a geometric process seen in the Lille example is its configuration adaptiveness. The shape of the city and the surrounding landscape is completely random, and the encircling fortifications bend to match this randomness, leading to Nouvel's claim that it is an early example of morphing. But once again there is no deliberate attempt at morphing going on. Since each component of a star fort is defined as a recursive relational transformation of the basic wall, Vauban only had to design the wall and the other parts aligned themselves as a result of the wall's configuration. If the outcome has artistic value, it is once again only incidental.

It is important to note that the Vauban extensions to star fortifications did not mean that the simple 3-part star fort became obsolete. In fact many simple star forts were built in the 18th and 19th century in America as the threat was low and the cities to be defended underdeveloped. The difference between a simple fort and Vauban's complex fort is one of depth and effectiveness, and there is a real cost-benefit choice to make. The star fort only became obsolete when the bunker replaced it, and the early bunkers reset the process of complex geometry genesis by being simple concrete shells in their early incarnations.

When we undertake to create symmetry in an urban environment, we want buildings to be as alike as possible while allowing for adaptation to context. If we understand geometric depth we can build in such a way that poor and expensive buildings have the same basic design in their first levels of geometry, but expensive buildings have many more scales of geometry nested within that basic design. It is not necessary for an entire city to be made of the same materials as materials are one of the last visible scales of geometry, and so we can have a city of mud bricks and marble buildings that nevertheless share 95% of their geometry and beautifully complement each other, while both poor and rich citizens have a home adapted to their situation.

We can look at these examples from Korean traditional architecture for an illustration.

On the left is a simple house and on the right is the tomb of a great king. Both buildings have the same design, but the building on the right has much greater depth in this design.

Another interesting comparison is between the Golden Gate bridge in San Francisco and the Verrazano Narrows bridge in New York.

The bridges are the same in design, but the Golden Gate bridge has more depth within this design, and is for this reason the more famous of the two bridges. That doesn't mean the Verrazano Narrows bridge isn't beautiful on its own.

And to make things as simple as they can get, we can compare a Sierpinski triangle with four levels of iteration with one that has six levels.

The fractal on the right has all the same elements as the one on the left, but also has more.

A lot of the residential buildings we create today would benefit from being more like the Verrazano Narrows bridge. They try to be more than a simple house for a simple family and end up covered in tacky, useless ornament that have obviously been forced into the design. Simplicity, if it is adapted to context, can create as beautiful a landscape as complexity. Postmodernistic nonsense geometry does not. We would be better served going back to the simplicity of 1950's international style modernism than what is being built by architects today. The best architects would reinvent it with greater depth.

Previous topics

• Complex geometry and structured chaos part 1
• Complex geometry and structured chaos part 2
• Design, configuration and natural form

References

Vauban, l'intelligence du territoire

A modern artist's homage to Vauban. This artist did not understand complex geometry.